选择排序

首先找到数组中最小的元素，将它和数组中的第一个元素交换位置。然后在剩下的元素中继续寻找最小的元素，将它和数组的第二个元素交换位置。如此往复直到将整个数组排序。选择排序不断地选择剩余元素中的最小值。

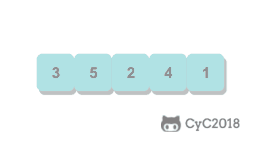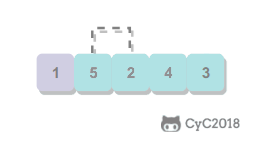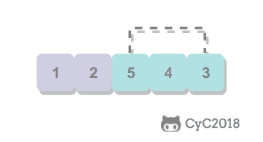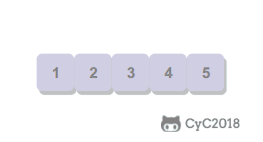
bc6be2d0-ed5e-4def-89e5-3ada9afa811a.gif

特点

  1. 运行的时间和输入无关。一个有序的数组或者主键全部相等的数组或者一个元素随机排列的数组所用的时间是一样长的。
  2. 数据的移动是最少的。每次交换都会改变两个数组元素的值，使用了 $N$ 次交换——交换次数和数组的大小是线性关系。

复杂度分析

  • 比较次数与初始状态无关，总比较次数：$N = (n - 1) + (n - 2) +…+ 1 = n × (n - 1 ) / 2$；
  • 交换次数
    • 最好情况是已经有序，交换 0 次；
    • 最坏情况是逆序，交换 n-1 ；
  • 时间复杂度
    • 最好：О(n²)
    • 最坏：О(n²)
    • 平均：О(n²)
  • 空间复杂度 O(1)
  • 不稳定

实现

1
2
3
4
5
6
7
8
9
10
11
12
public class Selection {
    public static void sort(Comparable[] a) {
        int n = a.length;
        for (int i = 0; i < n; i++) {
            int min = i;
            for (int j = i+1; j < n; j++) {
                if (less(a[j], a[min])) min = j;
            }
            exch(a, i, min);
        }
    }
}

插入排序

插入排序是一种简单有效的排序算法。它的工作原理是通过构造有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应的位置并插入。

特点

  • 插入排序所需的时间取决于输入元素的初始顺序。
  • 插入排序对于部分有序的数组十分高效。

复杂度分析

  • 比较
    • 最好：$N-1$（升序数组）
    • 最坏：$N\times(N-1)/2$（降序数组）
  • 交换
    • 最好：不需要交换（升序数组）
    • 最坏：交换 $N\times(N-2)$（降序数组）
  • 时间复杂度
    • 最好：$O(n)$
    • 最坏：$O(n²)$
    • 平均：$O(n²)$
  • 空间复杂度$O(1)$
  • 稳定

实现

1
2
3
4
5
6
7
8
9
10
public class Insertion {
    public static void sort(Comparable[] a) {
        int N = a.length;
        for (int i = 1; i < N; i++) {
            for (int j = i; j > 0 && less(a[j], a[j - 1]); j--) {
                exch(a, j, j - 1);
            }
        }
    }
}

改进

不需要交换的插入排序

在内循环中将较大的元素都向右移动而不总是交换两个元素（这样访问数组的次数就能减半）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 不需要交换的插入排序
public class InsertionB {
    public static void sort(int[] a) {
        int N = a.length;
        for (int i = 1; i < N; i++) {
            int t = a[i];
            int j;
            for (j = i; j > 0 && t < a[j - 1]; j--) {
                a[j] = a[j - 1];
            }
            a[j] = t;
        }
    }
}

插入排序的哨兵

哨兵：是能够省略判断条件的元素。哨兵机制是常见的规避边界测试的方法。

在插入排序中，先找出数组中最小的元素并置于数组的最左边，这样可以省略内循环中的 $j > 0$ 判断条件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 哨兵机制
 */
public static void InsertionC(int a[]) {
    int N = a.length;
    
    // 将最小的元素先放到数组的最左边作为哨兵
    int min = Integer.MAX_VALUE, min_index = 0;
    for (int i = 0; i < a.length; i++) {
        if (a[i] < min) {
            min = a[i];
            min_index = i;
        }
    }
    int t = a[0];
    a[0] = a[min_index];
    a[min_index] = t;
    
    // 内循环中的 j > 0 可以去掉
    for (int i = 2; i < N; i++) {
        for (int j = i; a[j] < a[j - 1]; j--) {
            t = a[j];
            a[j] = a[j - 1];
            a[j - 1] = t;
        }
    }
}

希尔排序

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序的核心思想是使数组中任意间隔为 h 的元素都是有序的，这样的数组称为 h 有序数组。

实现希尔排序只需要在插入排序的代码中将移动元素的距离由 1 改为 h 即可。

20170804062400495.gif

特点

  • 希尔排序的时间复杂度与递增序列密切相关，所以分析希尔排序的时间复杂度是个比较麻烦的事。
  • 希尔排序对于中等大小的数组表现良好，但是对规模非常大的数组不是最优选择。
  • 希尔排序实现简单，几乎任何排序工作在开始时都可以用希尔排序。若在实际使用中证明它不够快，再改成快速排序这样更高级的排序算法。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 希尔排序
 */
public static void sort(Comparable[] a) {
    int N = a.length;
    int h = 1;
    while (h < N / 3) {
        h = 3 h + 1;
    }
    while (h >= 1) {
        for (int i = h; i < N; i++) {
            for (int j = i; j >= h && less(a[j], a[j - h]); j -= h) {
                exch(a, j, j - h);
            }
        }
        h = h / 3;
    }
}