优先队列

优先队列支持两种最重要操作：删除最大元素和插入元素。优先队列可以通过有序或无序数组或链表实现，但是堆是实现优先队列最好的数据结构。

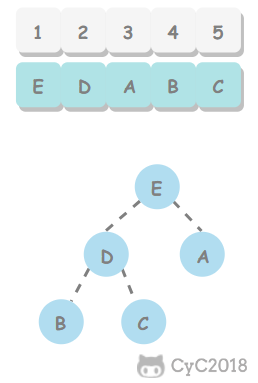
堆

定义

堆中某个结点的值总是大于等于它子节点的值，并且堆是一颗完全二叉树。当一颗二叉树的每个结点都大于等于它的两个子节点时，它被称为堆有序，根结点是堆有序的二叉树中的最大结点。

image.png

堆可以用数组来表示，这是因为堆是完全二叉树，而完全二叉树很容易存储在数组中，在数组中按照层级储存（不使用数组的第一个位置）。下标为 k 的结点的父结点下标为 k/2，而它的两个子结点的下标分别为 2k 或者 2k+1。在不使用指针的情况下，可以通过数组的索引在树中上下移动：向上一层则 k = k/2，向下一层则 k = 2k 或 2k+1。

一棵大小为 N 的完全二叉树的高度为 $log_2N$。

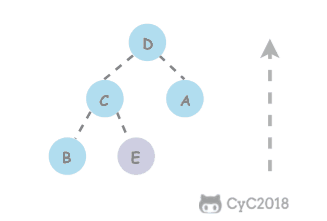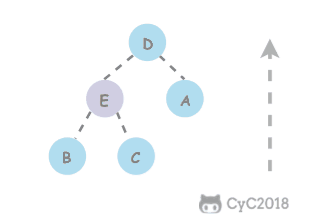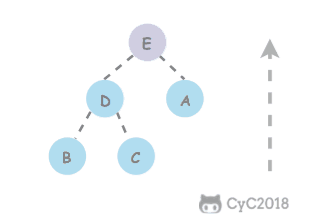
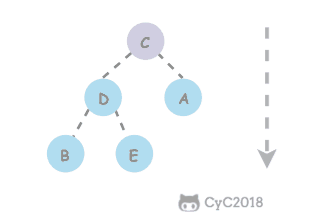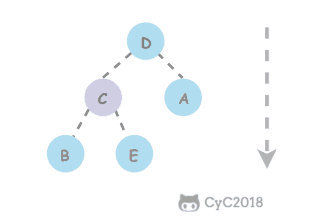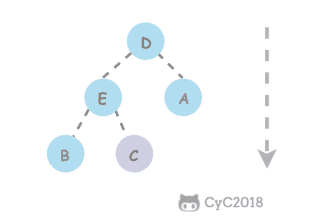
上浮

如果一个结点比它的父结点大，那么就交换这两个结点。交换后可能会比它的新父结点还大，因此需要重复相同的比较和交换来恢复秩序，这种操作是由下至上的堆有序化，称为上浮。

99d5e84e-fc2a-49a3-8259-8de274617756.gif

1
2
3
4
5
6
7
8
9
10
11
/**
 * 上浮
 */

private void swim(int k) {
    while (k > 1 && less(k/2, k)) {
        exch(k/2, k);
        // 向上一层
        k = k / 2;	
    }
}

下沉

在堆中，当一个结点比子结点小，需要不断地向下进行比较和交换。通过交换它和它的两个子结点中的较大值来恢复堆有序，这个过程称为下沉。

4bf5e3fb-a285-4138-b3b6-780956eb1df1.gif

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * 下沉
 */

private void sink(int k) {
    while (2 * k < N) {
        int j = 2 * k;
        if (j < N && less(j, j + 1)) j++;
        if (!less(k, j + 1)) break;
        exch(k, j);
        k = j;	// 下移一层
    }
}

插入元素

将新元素放入到数组的末尾，然后上浮到合适的位置

1
2
3
4
5
6
7
8
/**
 * 插入元素
 */

public void insert(Key k) {
    pq[++N] = v;
    swim(N);
}

删除最大元素

从数组的顶端删除最大的元素，并将数组的最后一个元素放到顶端然后下沉到合适的位置

1
2
3
4
5
6
7
8
9
10
11
/**
 * 删除最大元素
 */

public Key delMax() {
    Key max = pq[1];
    exch(1, N--);
    pq[N + 1] = null;
    sink(1);
    return max;
}

堆排序

堆排序可以分为两个阶段：

  • 在堆的构造阶段中，我们将原始数组重新组织安排进一个堆中。
  • 在下沉过程中，我们从堆中按递减顺序取出所有的元素并得到排序结果。

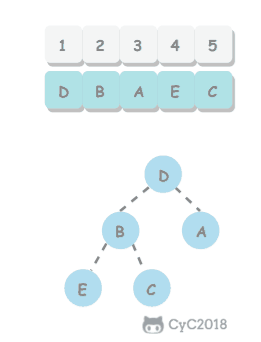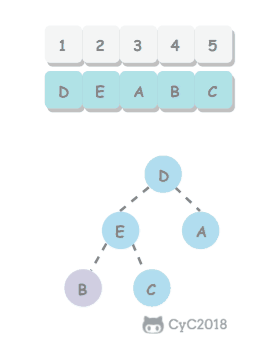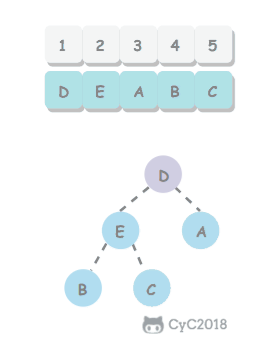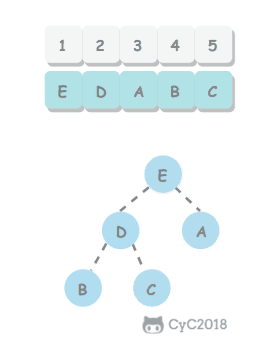
c2ca8dd2-8d00-4a3e-bece-db7849ac9cfd.gif

堆的构造

无序数组建立堆的最直接方式是从左到右遍历数组进行上浮操作。一个更高效的操作是从右至左进行下沉操作，数组的每个位置都已经是一个子堆的根结点了。如果一个结点的两个子结点都已经是堆，那么进行下沉可以让它们成为一个堆。这种方式我们只需要遍历数组的一半元素。

下沉排序

堆排序的主要工作都是在第二阶段完成的。我们将堆中的最大元素删除，然后放入堆缩小后数组中空出的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * 下沉排序
 */

public static void sort(Comparable[] a) {
    int N = a.length;
    for (int k = N / 2; k > 0; k--) {
        sink(a, k, N);
    }
    while (N > 1) {
        exch(a, 1, N--);
        sink(a, 1, N);
    }
}
public static void sink(Comparable[] a, int k, int n) {
    while (2 * k < n) {
        int j = 2 * k;
        if (j < n && less(a, j, j + 1)) j++;
        if (!less(a, k, j)) break;
        exch(a, k, j);
        k = j;
    }
}
private static void exch(Comparable[] a, int i, int j) {
    Comparable t = a[i - 1];
    a[i - 1] = a[j - 1];
    a[j - 1] = t;
}
private static boolean less(Comparable[] a, int i, int j) {
    return a[i - 1].compareTo(a[j - 1]) < 0;
}

改进

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * 不需要交换的堆排序
 */

public static void sort(Comparable[] a) {
    int N = a.length;
    for (int i = N / 2; i >= 1; i--) {
        sink(a, i, N);
    }
    System.out.println(Arrays.toString(a));

    while (N > 1) {
        exch(a, 1, N--);
        sink(a, 1, N);
    }
}

private static void sink(Comparable[] a, int k, int n) {
    Comparable t = a[k - 1]; // 用 t 将当前 k 的变量值保存
    while (2 * k < n) {
        int j = 2 * k;
        if (j < n && less(a, j, j + 1)) j++;
        if (t.compareTo(a[j - 1]) >= 0) break; // 当发现子节点的值小于 t 时，停止
        a[k - 1] = a[j - 1];
        k = j;
    }
    a[k - 1] = t; // 将 t 的值赋给 k 所在的位置
}

private static void exch(Comparable[] a, int i, int j) {
    Comparable t = a[i - 1];
    a[i - 1] = a[j - 1];
    a[j - 1] = t;
}

private static boolean less(Comparable[] a, int j, int j1) {
    return a[j - 1].compareTo(a[j1 - 1]) < 0;
}

复杂度

  • 时间复杂度
    • 最好：$O(N\log N)$
    • 最坏：$O(N\log N)$
    • 平均：$O(N\log N)$
  • 空间复杂度：$O(1)$
  • 不稳定

一个堆的高度为 $\log N$，因此在堆中插入元素和删除最大元素的复杂度都为 $\log N$。对于堆排序，由于要对 N 个节点进行下沉操作，因此复杂度为 $N\log N$。

现代系统的许多应用很少使用堆排序。因为它无法利用缓存。数组元素很少和相邻的其它元素进行比较，因此无法利用局部性原理，缓存未命中的次数很高。