原地归并方法

原地归并方法是不同归并排序的基础。首先将所有元素复制到了aux[]中，然后再归并回a[]中。在第二个 for 循环中进行了 4 个条件判断：

  • 左半边用尽，取右半边的元素；
  • 右半边用尽，取左半边的元素；
  • 右半边的当前元素小于左半边的当前元素，取右半边的元素；
  • 右半边的当前元素大于等于左半边的元素，取左半边的元素；
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    /**
     * 原地归并
     */

    public static void merge(Comparable[] a, Comparable[] aux, int start, int mid, int end) {
    	int i = start, j = mid + 1;
        
        for (int k = start; k <= end; k++) {
        	aux[k] = a[k];
        }
        
        for (int k = start; k<= end; k++) {
        	if (i > mid) a[k] = aux[j++];
            else if (j > end) a[k] = aux[i++];
            else if (less(a[j], a[i])) a[k] = aux[j++];
            else a[k] = a[i++];
        }
    }

归并排序

自顶向下

自顶向下的归并排序应用了分治的思想，要对数组 a 排序，现将数组分为a[start, mid]和a[mid + 1, end]两个部分，分别通过递归的调用来将它们单独排序，最后将有序的子数组归并为最终的结果。

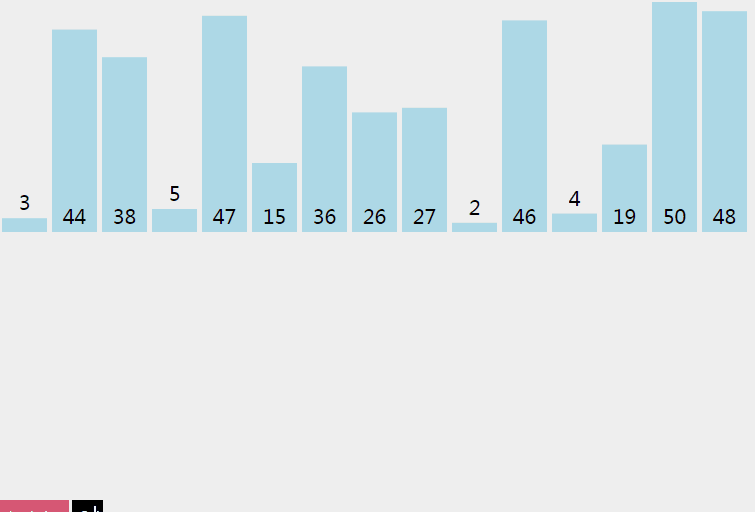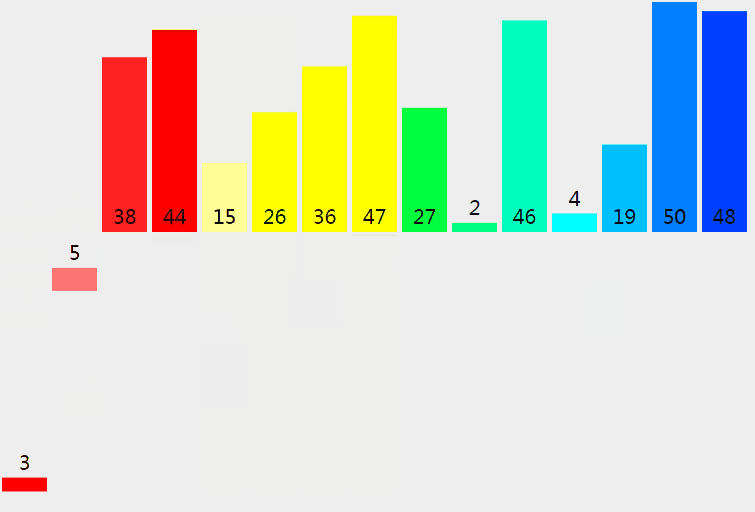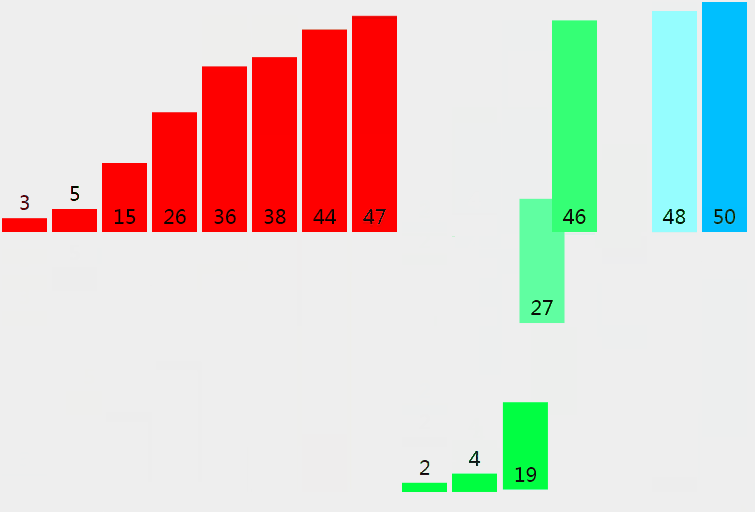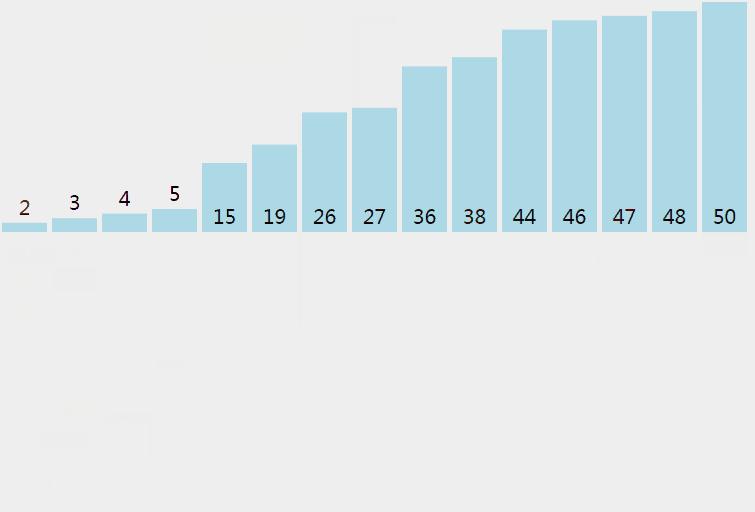
20161009190940095.gif 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 自顶向下归并
 */

public class Merge {
    // 归并所需的辅助数组
    private static  Comparable[] aux;

    public static void sort(Comparable[] a) {
        // 一次性分配空间
        aux = new Comparable[a.length];
        sort(a, aux, 0, a.length - 1);
    }

    private static void sort(Comparable[] a, Comparable[] aux, int start, int end) {
        if (end <= start) return;

        int mid = (start + end) / 2;
        // 将左半边排序
        sort(a, aux, start, mid);
        // 将右半边排序
        sort(a, aux, mid + 1, end);
        // 归并结果
        merge(a, aux, start, mid, end);
    }
}

自底向上的归并排序

实现归并排序的另一种方法是先归并那些微型数组，然后在成对归并得到的子数组，如此这般多次的遍历整个数组，直到我们将整个数组合并到一起。

自底向上的归并排序比较适合链表组织的数据。

可以将链表按照大小为 1 的子链表进行排序，然后是大小为 2 的链表，然后是大小为 4 的子链表等。

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * 自底向上归并
 */

public class MergeBU {
    private static Comparable[] aux;
    
    public static void sort(Comparable[] a) {
        int N = a.length;
        aux = new Comparable[N];
        
        for (int size = 1; size < N; size = 2 * size) {
            for (int start = 0; start < N - size; star += 2 * size) {
                merge(a, start, start + size - 1, Math.max(start + 2 * size - 1, N - 1);
            }
		}
	}
}

特点

  • 归并排序的空间复杂度不是最优的，辅助数组 aux 使用的空间和数组的大小成正比。
  • 和选择排序一样，归并排序的性能不受输入数据的影响，但是表现比选择排序好。
  • 自底向上和自顶向上的归并排序所用的比较次数和数组访问次数相同，只是顺序不同。

复杂度分析

  • 时间复杂度
    • 最好：$O(n\log n)$
    • 最坏：$O(n\log n)$
    • 平均：$O(n\log n)$
  • 空间复杂度 $O(n)$
  • 稳定