前言
快速排序是另外一种分治的排序算法,它将一个数组分为两个子数组独立地排序。
快速排序和归并排序是互补的:
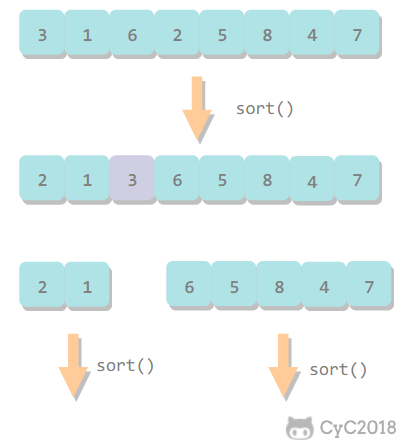
- 归并排序将数组分为两个子数组分别排序,并将有序的子数组归并以将整个数组排序。
- 快速排序排序数组的方式是当两个子数组都有序时,整个数组同时自然有序。
- 区别在于:归并排序的递归调用在归并处理整个数组之前,快速排序的递归调用在处理整个数组之后。
实现
基本方法
1 | /** |
快速排序的关键在于切分方法partition()的实现。
切分方法
我们通常会选取a[start]作为切分元素分割数组:我们从数组的左端开始向右扫描直到找到一个大于等于切分元素的元素,再从数组的右端开始向左扫描直到找到一个小于等于切分元素的元素。这两个元素并没有排定,因此交换它们的顺序。如此继续,我们就可以保证左指针 i 的的左侧元素都小于等于切分元素,右指针 j 的右侧元素都大于等于切分元素。当两个指针相遇时,我们只需要将a[start]和a[j]交换然后返回 j 就可以。
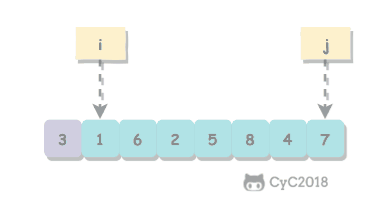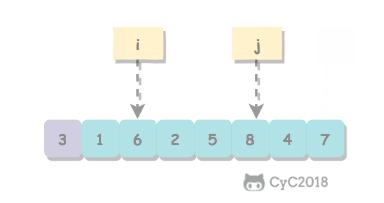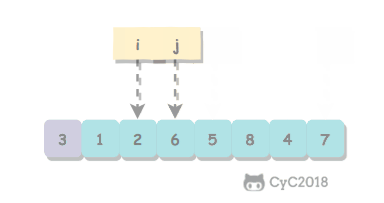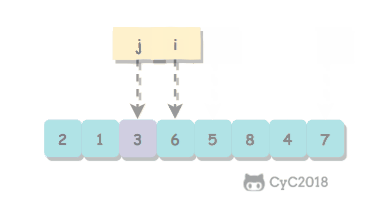
通过切分方法,数组满足了三个条件:
- 对于切分元素,它经过切分方法后已经排定,它的正确顺序在数组的 j 位置;
a[start]....a[j - 1]都小于等于切分元素;a[j + 1]....a[end]都大于等于切分元素;1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16/**
* 切分方法
*/
private static int partition(Comparable[] a, int start, int end) {
int i = start, j = end + 1;
Comparable v = a[start];
while (true) {
while (less(a[++i], v)) if (i == end) break;
while (less(v, a[--j])) if (j == start) break;
if (i >= j) break;
exch(a, i, j);
}
exch(a, start, j);
return j;
}
复杂度
时间
时间复杂度:
- 最好:$O(n\log n)$
- 最坏:$O(n^2)$
- 平均:$O(n\log n)$
最好情况:数组每次都正好对半分。比较次数正好满足分治递归的 $C_N = 2C_{N/2} + N$。
$C_{N/2}$ 表示将两个子数组排序的成本,$N$表示切分元素和数组所有元素比较的成本。
$C_N \to n\log n$
最坏情况:第一次从最小的元素开始切分,第二次从第二小的元素开始切分,如此递归。每次切分后两个子数组中总有一个是空,比较次数为 $(n - 1) + (n - 2) +…..+ 1 = n(n - 1) / 2 \to n^2$。
在快速排序之前将数组随机排序可以避免切分不平衡,随机排序可以将切分不平衡的可能性降到最低。
空间
主要考虑递归调用所占用的栈空间。
- 最好:$O(\log n)$(对半分)
- 最坏:$O(n)$
- 不稳定
改进
哨兵
由于切分元素本身就是一个哨兵,所以左侧边界的检查是多余的。可以在打乱数组之后将数组的最大值放在数组的末尾充当所有子数组的哨兵,这样子可以去掉右侧边界的检查。
切分元素不会小于自己,所以可以作为一个哨兵。
1 | /** |
切换到插入排序
因为快速排序在小数组中也会递归调用自己。对于小数组,插入排序比快速排序的性能更好,因此在小数组中可以切换到插入排序。
只需要将if(end <= start) return;改成if(end <= start + M) { Insertion.sort(a, start, end); return;}。
转换参数 M 的最佳值是和系统相关的,一般来说 5~15 之间的任意值在大多数情况下都可以满足。
JDK 内置的 M 设置为 47
三取样切分
最好的情况下是每次都能取数组的中位数作为切分元素,但是计算数组中位数的代价很高。研究发现取三个元素并将大小居中的元素作为切分元素的效果最好。
1 | /** |
三向切分
在存在大量元素的情况下,快速排序的递归性会使元素全部重复的子数组经常出现,这里存在很大的改进空间,将当前实现的线性对数级的性能改进到线性级别。
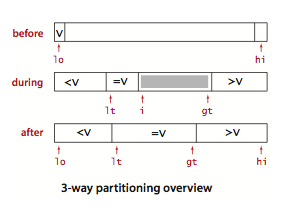
从左到右维护三个指针:
- lt:
a[start]...a[lt - 1]都小于 v; - gt:
a[gt + 1.....end]都大于 v; - i:
a[lt]...a[i - 1]都等于 v,a[i].....a[gt]未确定。
一开始i == start,之后对a[i]进行三向比较:
a[i] < v:a[lt]和a[i]交换,lt++和i++;a[i] > v:a[gt]和a[i]交换,gt--;a[i] == v:i++;
1 | /** |
这种快排的方式在重复元素不多的普通情况下比二分法使用了很多次交换。
快速三向切分
将重复的元素放置于子数组的两端的方式来实现一个最优的三向切分排序算法:
- 使用两个索引 p 和 q,使
a[start]...a[p-1]和a[q+1....a[end]都和a[start]相等。 - 使用两个索引 i 和 j,使
a[p]...a[i-1] < a[start],a[j+1...a[q] > a[start]。 - 在内循环中,
a[i]和 v 相等时将其与a[p]交换,在a[j]和 v 相等时和a[q]交换。这里实现的代码和第一段的代码是等价的,因为这里额外的交换用于和切分元素相等的元素,而第一段中的代码将额外的交换用于和切分元素不等的元素。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41/**
* 快速三向切分
*/
private static void sort(int[] a, int start, int end) {
if (end <= start) return;
int v = a[start];
int p = start, q = end + 1;
int i = start, j = end + 1;
while (true) {
while (i < end && a[++i] < v);
while (a[--j] > v);
if (i >= j) break;
exch(a, i, j);
if (a[i] == v) {
++p;
exch(a, p, i);
}
if (a[j] == v) {
--q;
exch(a, q, j);
}
}
exch(a, start, j);
int lt = j - 1, gt = j + 1;
int k = start + 1, m = end;
while (k <= p) {
exch(a, lt, k);
++k;
--lt;
}
while (m >= q) {
exch(a, gt, m);
--m;
++gt;
}
sort(a, start, lt);
sort(a, gt.end);
}