前言
二叉查找树在常见的情况下,查找和插入的效率可以达到对数级别,但是在最坏的情况下会到达线性级别。总的来说,二叉查找树的运行时间取决于树的形状,树的形状取决于键插入的先后顺序。平衡查找树能够保证无论插入的顺序如何,树的运行时间都是对数级别的。
2-3 查找树
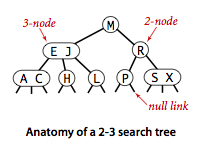
一颗 2-3 查找树或为一颗空树,或者由一下的结点组成:
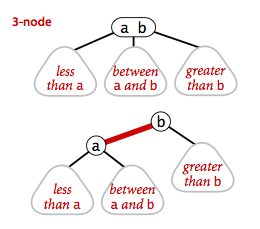
- 2-结点:含有一个键和两条链接,左链接指向的子树的键值都小于该结点,右链接指向的子树的键都大于该节点;
- 3-结点:含有两个键和三条链接,左链接指向的子树的键都小于该结点,中链接指向的子树的键位于该结点两个键值中间,右链接指向的子树的键都大于该结点;
查找
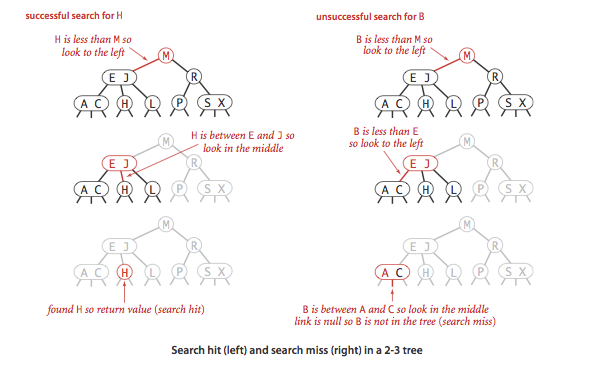
要判断一个键是否存在于树中,先将该键和根结点中的键比较。如果和其中的任意一个相等,则查找命中;否则根据比较的结果找到指向相对应区间的链接,并在其指向的子树中继续递归查找。
插入
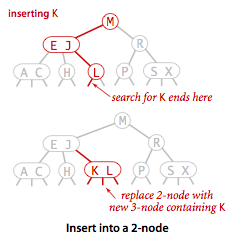
向 2-结点中插入新键
- 先进行一次未命中的查找,结束于一个 2-结点
- 将 2-结点替换为 3-结点,然后将键值保存在其中
向根 3-结点中插入新键
- 将新键存入结点中并转换为 4-结点
- 将 4-结点分解为 3 个 2-结点组成的 2-3 树
向 2-结点的 3-结点中插入新键
- 构造一个临时的 4-结点,分解为 3 个 2-结点
- 将中间移动到 2-结点中
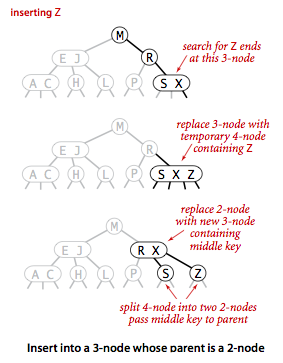
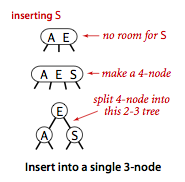
向 3-结点的 3-结点中插入新键
- 构造一个临时的 4-结点并分解为 3 个 2-结点
- 将中键插入到父 3-结点中,重复 1
过程:向上不断分解 4-结点并将中键插入到更高层的父结点中,直到遇到一个 2-结点或者是到达根结点。
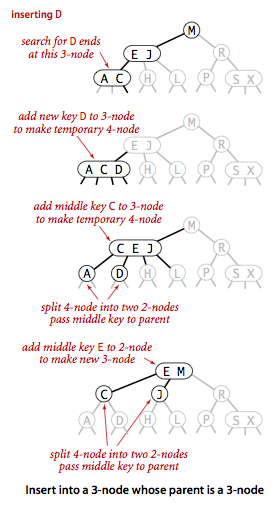
分解根结点
如果从插入结点到根结点的路径上全都是 3-结点,根结点最后会变为 1 个 4-结点。将 4-结点分解为 3 个 2-结点,最终让树的高度+1。
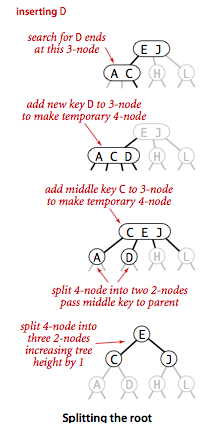
构造性质
2-3 插入算法的根本在于这些变换都是局部的:除了相关的结点和链接之外不必修改或者检查树的其他部分。在树中的任意地方只要符合相对应的模式,变换都可以进行。所以局部变换不会影响树的全局有序性和平衡性,任意空链接到根结点的路径长度都是相等的。
标准的二叉树是由上向下生长,2-3 树是由下向上生长的。
1 | 命题 F 在一颗大小为 N 的 2-3 树中,查找和插入操作访问的结点必然不超过 lgN 个。 |
红黑树
定义
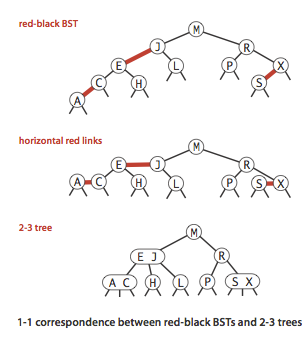
2-3 树的直接实现很难,所以通过红黑二叉查找树来间接实现。
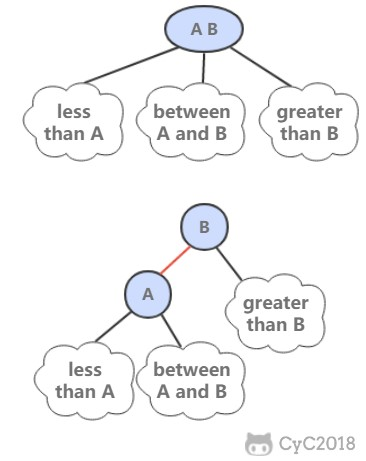
红黑树中的链接分为两种类型:红链接将两个 2-结点连接起来构成一个 3-结点,黑链接则是 2-3 树中的普通链接。
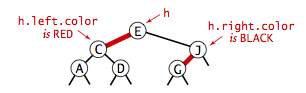
红黑树的性质:
- 红链接均为左链接;
- 没有任何一个结点同时和两条红链接相连;
- 该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同;
如果将红链接相连的结点合并,得到的就是一颗 2-3 树。同样,如果将一颗 2-3 树中的 3-结点画作由红色左链接相连的两个 2-结点,那么不会存在能够和两条红链接相连的结点,且树是完美黑色平衡的。
基本实现
将链接的颜色保存在Node数据类型的布尔变量color中,如果指向它的链接是红色,则为true,如果链接为黑色,则为false。约定空链接为黑色。
1 | public class RedBlackBST<Key extends Comparable<Key>, Value> { |
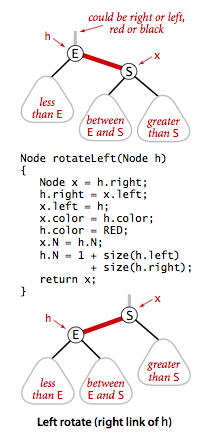
旋转
假设有一条红色的右链接需要被转化为左链接,我们需要进行左旋转。同理还有右旋转。
左旋转:将根结点选为两个键中较大的键
右旋转:将根结点选为两个键中较小的键
旋转可以保持红黑树的两个重要性质:有序性和完美平衡性
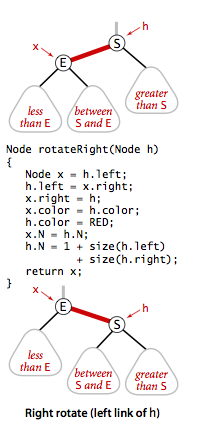
1 | // 左旋转 |
在旋转结束后,返回的链接可能是左链接或者右链接,但是我们总会将它赋予父结点中的链接,这个链接可能是红色也可能是黑色。所以存在两条连续的红链接,算法会继续通过旋转修正这种情况。
颜色转换
一个 4-节点在红黑树中表现为一个节点的左右子节点都是红色的。分裂 4-节点除了需要将子节点的颜色由红变黑之外,同时需要将父节点的颜色由黑变红,从 2-3 树的角度看就是将中间节点移到上层节点。
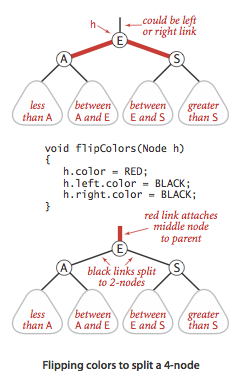
1 | private void flipColors(Node h) { |
根结点总是黑色
当左右链接都为红色时,从 2-3 树的角度看,意味着两个子节点和父结点组成了一个 4-结点,颜色反转操作相当于将 4-结点分裂为三个 2-结点,当该 4-结点在树中间时不会对树的高度产生影响,但是当 4-结点出现在根结点时,我 们会将中间键的 2-结点弹出,此时树的黑链接高度加一。
我们每次插入后都将根结点设为黑色,树的黑链接高度同时加一。
插入
在使用二叉查找树的插入算法将键插入到正确的位置后,在沿着插入点到根结点的路径向上移动时在所经过的每个结点中顺序完成以下操作:
- 如果右子节点是红色而左子节点是黑色,进行左旋转;
- 如果左子节点是红色且它的左子节点也是红色的,进行右旋转;
- 如果左右子节点都为红色,进行颜色转换;
1 | public void put(Key key, Value value) { |
除了递归调用后的三条if语句,红黑树中put()的递归实现和二叉查找树中的put()的实现完全相同。
删除最小键
为了保证树的完美平衡性,沿着左链接向下进行变换,确保当前结点不是一个 2-结点。最后能够得到一个含有最小键的 3-结点或者 4-结点,将最小键删除后,向上分解所有的临时 4-结点。
删除键
在查找路径上进行和删除最小键相同的变换同样可以保证在查找过程中任意当前节点均不是 2-节点。如果被查找的键在树的底部,我们可以直接删除它。如果不在,我们需要将它和它的后继节点交换,就和二叉查找树一样。因为当前节点必然不是 2-节点,问题已经转化为在一棵根节点不是 2-节点的子树中删除最小的键,可以直接使用上文的算法。删除之后我们需要向上回溯并分解余下的 4-节点。
查找
红黑树也是二叉查找树,同时查找的操作不涉及颜色,所以查找的方法和普通二叉查找树相同,但是应为树是平衡的,所以get()的速度更快。
1 | public Value get(Key key) { |
复杂度分析
无论键的插入顺序如何,红黑树都几乎是完美平衡的,所以所有基于红黑树的符号表实现都能保证操作的运行时间为对数级别(范围查找除外,它需要的额外时间和返回的键的数量成正比)。