前言

从算法的逻辑上来说，二叉树的查询 (log2_N) 和插入效率 (log2_N) 已经很高。但是在实际的应用当中，我们不能将索引全部加载到内存之中，只能逐一的加载每一个磁盘页。这里的磁盘页就对应索引树的结点，相比于内存的比较和读取来说，磁盘 I/O 存取消耗的时间要高很多，所以判断一个数据结构是否适合于索引问题的关键就是计算产生的磁盘 I/O 次数。

B-树

B-树是对 2-3 树的一种补充，是一种多路平衡查找树。一个 M 阶的 B 树（M 取决于磁盘页的大小）的特点：

  • 根结点的子节点数量在 [2, M]；
  • 每个中间结点包含了 k-1 个元素和 k 个子节点，其中 k∈ [M/2, M]；
  • 每一个叶子节点包含了 k-1 个元素，其中 k∈ [M/2, M]；
  • 所有的叶子节点都在同一层；
  • 每个节点中的元素从小到大排列，节点当中 k-1 个元素正好是 k 个孩子包含的元素的值域分划。

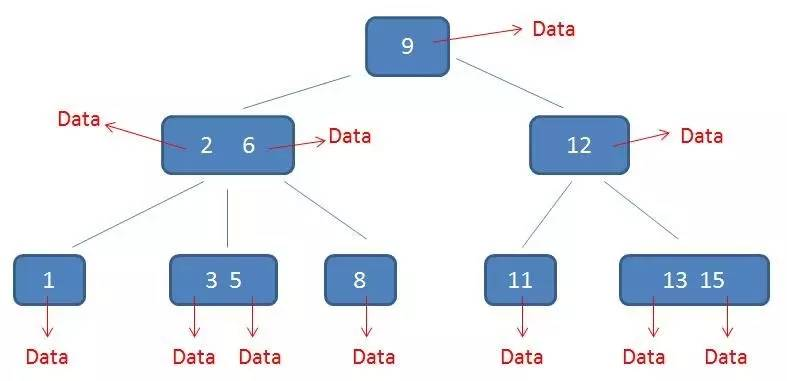
对于大量的数据来说，采用 B-树的结构是非常合适的。因为 B-树的一个结点可以存放更多的值，所以 B-树会比二叉树更矮、更胖，到达叶子结点所需要的磁盘 I/O 次数也更少。

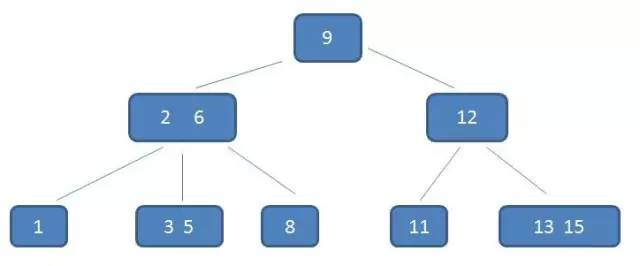
image.png

查找

下面 3 幅图描述了在一个 3 阶的 B-树中，如何查找到 5:

第一次磁盘 I/O 并在内存中和 9 比较
第 2 次磁盘 I/O 并和 2、6 比较
第 3 次磁盘 I/O 并和 3、5 比较

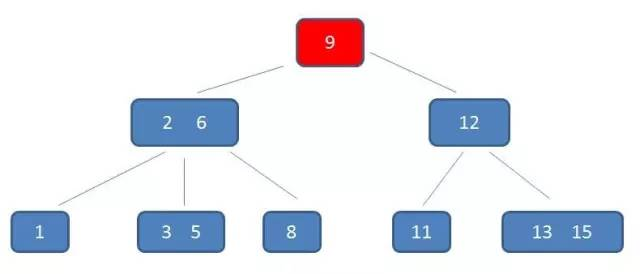
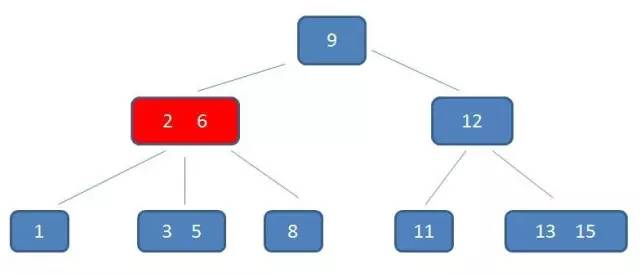
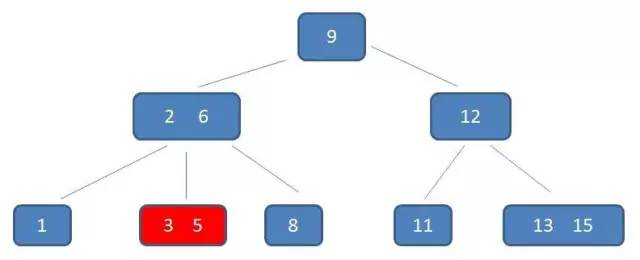
从比较的次数来看，B-树没有和二叉树有着太多的差异。但是因为 B-树中的一个结点可以存放多个元素，所以磁盘 I/O 的次数可以少很多，同时内存中的比较耗时相对来说可以忽略，因此查找的性能会比二叉树好。

插入

B-树的插入模式和 2-3 树相似，都是将结点转换为临时结点，然后不断向上递归直到根结点。
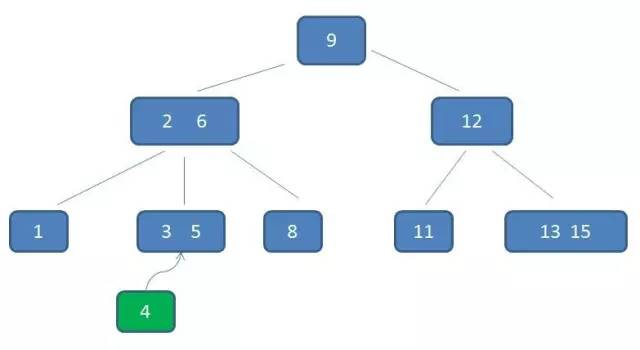
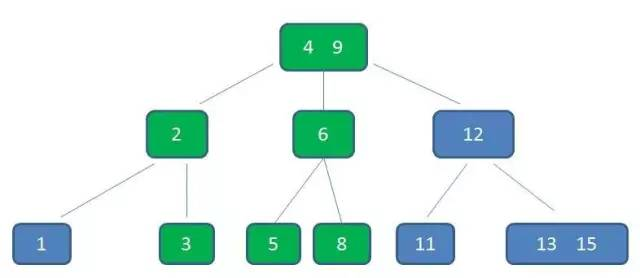
以向图中的 B-树插入 4 为例：首先自顶向下查找 4 的结点位置，发现 4 应该插入到 (3, 5) 结点中。3 阶 B-树的结点最多含有两个元素，所以向父结点插入 4 同时将剩下的 (3, 5) 结点拆分，创建一个临时 4 结点。然后再将 4 插入到根结点升级为两元素节点 (4, 9)。将剩下的 (2, 6) 结点拆分，节点 6 独立为根节点的第二个孩子。

删除

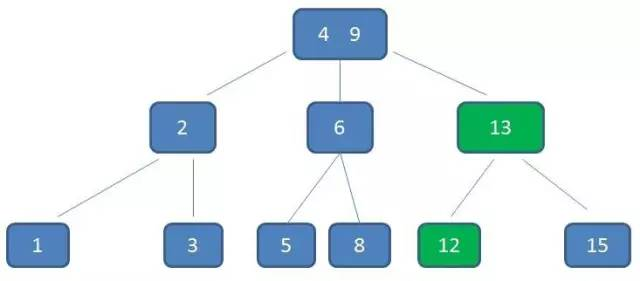
以删除 11 结点为例，首先自顶向下查找元素 11 所在的位置。删除 11 结点后，结点 12 只有一个右子结点，所以找出 12，13，15 三个数中的中位数 13 取代 12，同时 12 结点左下移成为一个子节点（左旋操作）。

找到 11 结点所在位置
找出 12、13 和 15 中的中位数
左旋操作

B+树

B+树是 B-树的一个变体，有着比 B-树更好的查询性能。一个 M 阶的 B+树（M 同样取决于磁盘页的大小）和 B-树之间的区别在于：

  • 有 k 个子树的中间结点包含了 k 个元素，而在 B-树中的元素该中间结点包含了 k-1 个元素；
  • B+树中的中间结点仅用于索引，不保存数据，所有的数据都保存在了叶子结点中；
  • 所有的中间结点元素都同时存在于子节点，在子节点中是最大（或最小）元素；
  • 所有的叶子结点包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身按照元素的关键字大小升序链接构成一个有序链表；
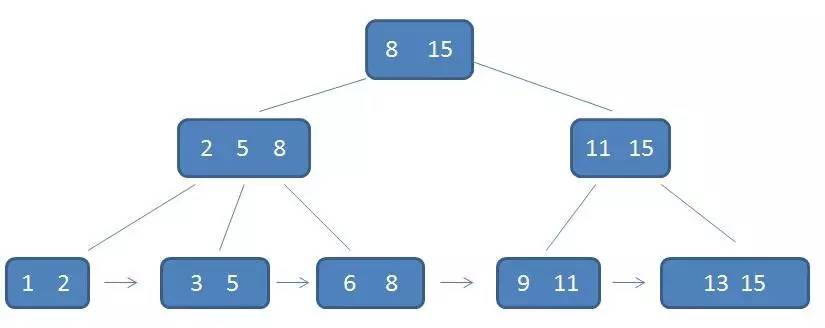
image.png

根结点的最大元素等同于整个 B+树的最大元素；由于父结点的元素都出现子节点，因此所有的叶子结点包含了全部元素的信息，每一个叶子结点还带有指向下一个结点的指针，形成了一个有序的链表。

在 B-树中，无论中间节点还是叶子节点都带有卫星数据（索引元素所指向的数据记录），而Ｂ+树中间节点没有卫星数据，只有索引，这就意味着同样大小的磁盘页可以容纳更多节点元素，在相同的数据量下，B+树更加“矮胖”，IO 操作更少。

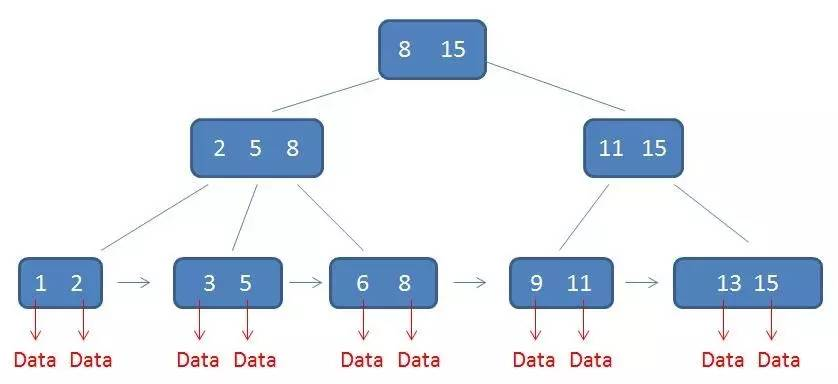
image.png
B-树中间结点和叶子结点都带有卫星数据
image.png
B+树只有叶子结点才带有卫星数据

查找

以查找元素 3 为例，记录 B+树中的磁盘 I/O 过程：

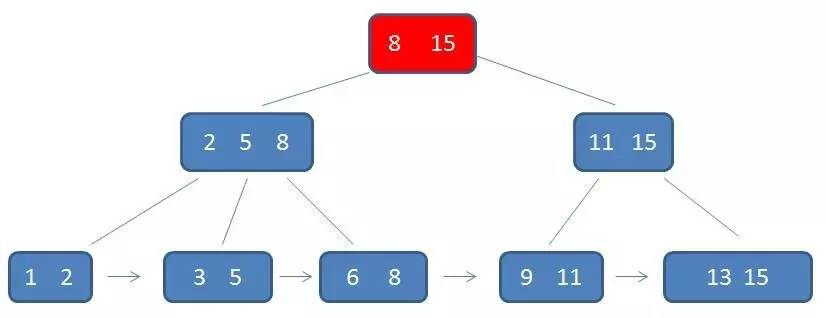
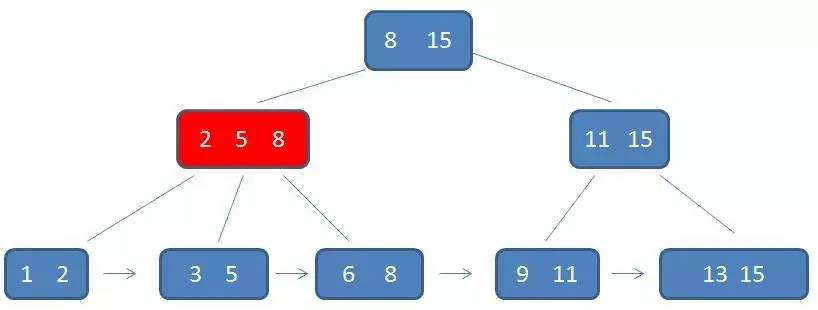
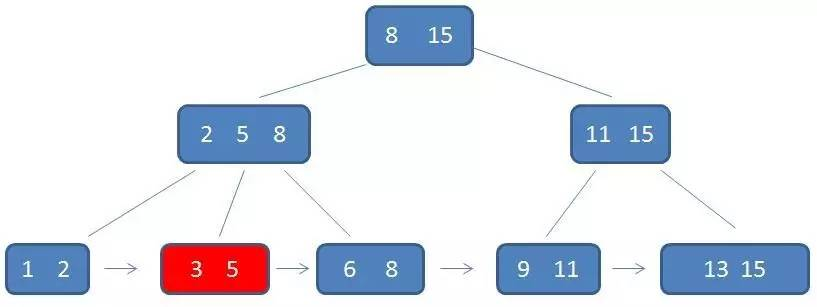
image.png image.png image.png

B+树的查询必须最终查找到叶子结点；在 B-树中只要找到目标元素即可，所以最终可能查询到中间结点或者是叶子结点。对比来看，B+树的查找性能是稳定的，而 B-树的查找性能不稳定（最好情况是查找根结点，最坏情况是查到叶子结点）。

在相同的数据量的情况下，由于一个结点可以存放更多的数据，B+树的深度会比 B-树更低，所以查询所需要的磁盘 I/O 更少。同样的磁盘页大小，B+树可以存储更多的元素。

范围查找

由于 B+树的叶子节点构成了一条有序链表，因此 B+树的范围查找要比 B-树简单的多，而 B-树需要铜鼓中序遍历来完成范围的查找，效率会低很多。下面以查询范围为 3～11 的元素为例：

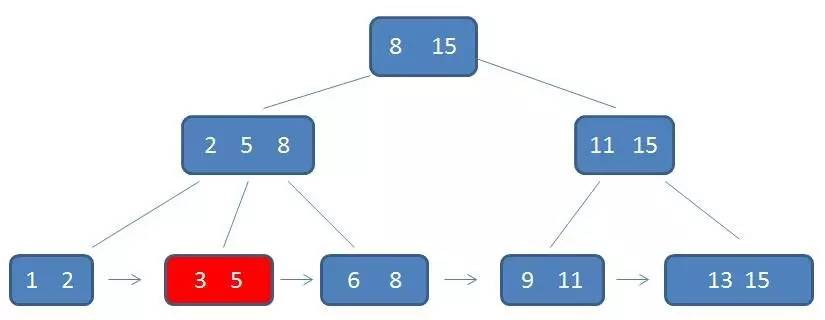
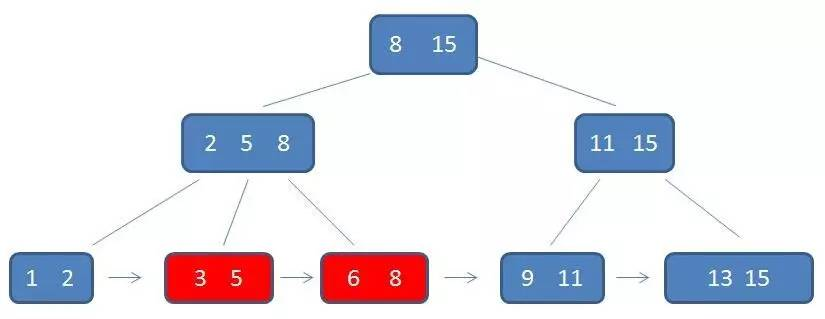
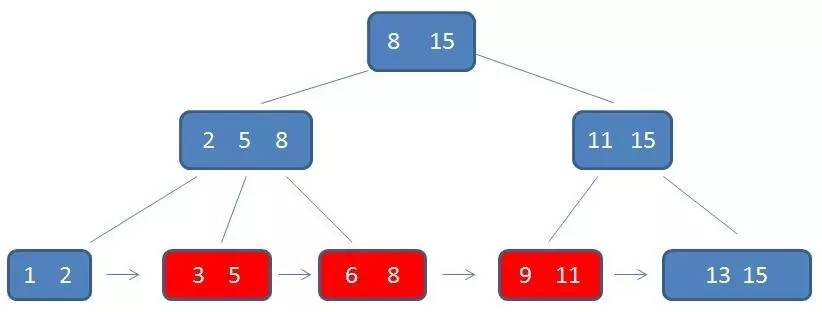
image.png
自顶向下，查找到范围的下限 3
image.png
通过链表指针，遍历到元素 6、8
image.png
通过链表指针，遍历到元素 9、11，遍历结束

总结

为了减少磁盘的 I/O 次数，必须降低树的深度，将原本”瘦高”的树改造成为“矮胖”，使得相同的磁盘页可以容纳更多的结点元素，因此出现了 B-树。B+树是 B-树的变体，在 mysql 中采用的是 B+树，其相比 B-树的优势在于：

  • 单一结点存储的元素更多，查询所需要的磁盘 I/O 更少；
  • 所有查询都会查找到叶子节点，查询性能更稳定；
  • 所有叶子节点形成了一个有序链表，便于范围查询；

除了 B-tree，平时还会听到有 B*树的概念，同样 B*树是 B+树的一个变体，相比 B+树的不同之处如下：

  • 将结点的最低利用率从 1/2 提高到 2/3。
  • 在 B+树基础上，为非叶子结点也增加链表指针：B+树当一个结点满时，会分配一个新的结点，并将原结点中 1/2 的数据复制到新结点，最后在父结点中增加新结点的指针；B*树当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，而如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制 1/3 的数据到新结点，最后在父结点增加新结点的指针。

参考

  1. 漫画：什么是 B+树？
  2. 漫画：什么是 B-树？